PRML - 机器学习视角下的概率论核心 • Jaison's ink

贝叶斯曲线拟合#

公式 1.68：预测分布的积分定义
$p(t|x, \mathbf{x}, \mathbf{t}) = \int \underbrace{p(t|x, \mathbf{w})}_{\text{模型预测}} \cdot \underbrace{p(\mathbf{w}|\mathbf{x}, \mathbf{t})}_{\text{参数后验}} d\mathbf{w}$

$p(t|x, \mathbf{x})$ 是最终我们想预测的联合概率
$p(t|x, \mathbf{w})$ 是以w为参数时我们对t的预测
$p(\mathbf{w}|\mathbf{x}, \mathbf{t})$ 则体现了我们对参数取w的信任程度
我们将所有可能的w算一遍 $p(t|x, \mathbf{w})$ ，然后根据我们对该w的信任程度后验概率 $p(\mathbf{w}|\dots)$ ）进行加权求和（积分），得到最终的联合概率。
这体现了这样一种思想：
我们不是要找一个“最优的参数”来预测，而是要综合所有可能的参数来预测。

即

新的预测 $t$ 的概率分布 = $\sum$ ( 某个特定参数 $\mathbf{w}$ 下的预测 $\times$ 我们有多信任这个 $\mathbf{w}$ )

公式 1.69：预测分布的形式
（这里假定了先验和似然都是高斯分布）
$p(t|x, \mathbf{x}, \mathbf{t}) = \mathcal{N}(t | m(x), s^2(x))$

解释：积分的结果是什么样子的？
因为我们的先验是高斯，似然是高斯，根据高斯的共轭性质，积出来结果依然是一个高斯分布。
既然是高斯分布，我们只需要找出它的均值 $m(x)$ 和 方差 $s^2(x)$ 就能描述它。

公式 1.70：预测均值

$m(x) = \mathbf{m}_N^T \phi(x)$

解释：新的预测均值 = 后验均值参数 $\mathbf{m}_N$ $\times$ 基函数 $\phi(x)$ 。
这和点估计（MAP）的结果是一样的。也就是说，虽然我们考虑了所有 $\mathbf{w}$ ，但在预测的“中心位置”上，还是那个最可能的参数说了算。

公式 1.71：预测方差（核心公式！）
$s^2(x) = \underbrace{\frac{1}{\beta}}_{\text{数据噪声}} + \underbrace{\phi(x)^T \mathbf{S}_N \phi(x)}_{\text{参数不确定性}}$

解释：预测的不确定性（方差）由两部分组成：
1. 数据固有的噪声 ( $\frac{1}{\beta}$ )：即使模型完美，数据本身也有随机误差，这部分无法消除。
2. 模型参数的不确定性 ( $\phi(x)^T \mathbf{S}_N \phi(x)$ $ϕ (x)^{T} S_{N} ϕ (x)$ )：这是贝叶斯独有的。
  - $\mathbf{S}_N$ 是参数 $\mathbf{w}$ 的协方差矩阵/
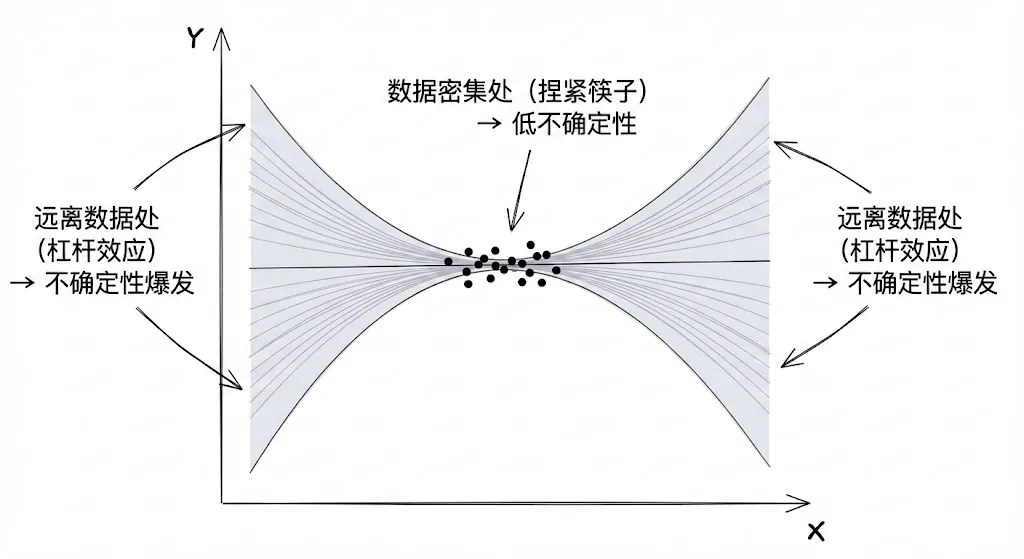
  - 这就解释了为什么贝叶斯回归的置信区间呈现**“香肠状”**：在数据密集的地方，参数估计准（ $\mathbf{S}_N$ 作用小），方差小；在远离数据的地方，方差会变大。

维度灾难(Curse of dimensionality)#

低维度上的很多直觉不能直接拓展到高维度上。

考虑D维空间中半径为r的球体在r = 1 - $\epsilon$ 到r = 1之间的部分在球的总体积中的占比。

D维空间中体积正比于 $r^D$
$V_D(r) = K_Dr^D$
$\frac{V_D(1) - V_D(1 - \epsilon)}{V_D(1)} = 1 - (1 - \epsilon)^D$
当D趋于无穷大，即使 $\epsilon$ 很小，占比也趋近于1.
因此在高维空间中，球体大部分的体积集中于在球体表面附近的薄壳中。

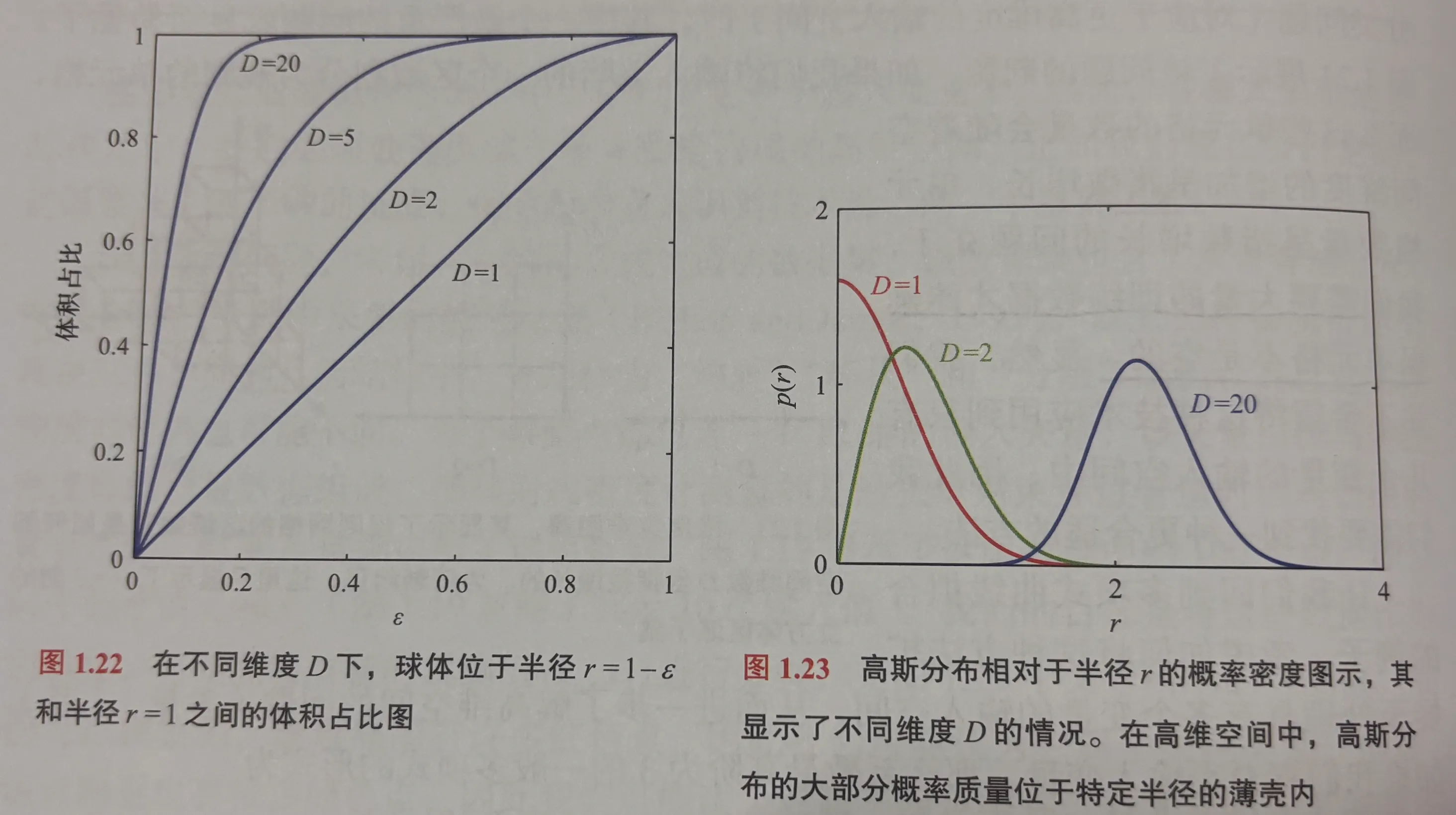
考虑一个多维度的高斯分布，其类似于一个球。
虽然单看一个维度中间部份的“密度”最大，但高维情况下，大部分质量仍然在一个空心球壳附近，所以如果随机取数，也更有可能取在这个球壳上。
“高斯薄壳”的密度峰值：
$\hat{r} \simeq \sqrt{D} \sigma \quad$

这引出一个可怕的后果：
在很多机器学习算法（如 KNN、K-Means）中，我们依赖**“距离”**来判断相似度。但是因为这个“薄壳效应”：

所有随机样本都落在同一个半径的壳上。
这就导致所有点之间的距离看起来都差不多！
“最近邻”和“最远邻”的区别变得微乎其微，导致基于距离的算法在高维空间失效。

不要用三维直觉去想象高维空间，高维空间里，中心是空的，大家都在壳上。